Нерка vs Кета — Новеллы и устареллы — LiveJournal

?

Нерка vs Кета

alexod

July 22nd, 2015

На самом деле и та и та офигенные, но ИМХО для бутеров кета самое-то.
Ну а вот хар-ки одной и второй:

Калорийность Красной икры кеты 249 кКал.

Энергетическая ценность продукта Красная икра кеты (Соотношение белков, жиров, углеводов):

Белки: 31.5 г. (~126 кКал)
Жиры: 13.2 г. (~119 кКал)
Углеводы: 1 г. (~4 кКал)

Энергетическое соотношение (б|ж|у): 51%|48%|2%

Пропорции продукта. Сколько грамм?

в 1 чайной ложке 12 граммов
в 1 столовой ложке 35 граммов

Пищевая ценность

Зола 7.4 г
Холестерин 310 мг
Насыщеные жирные кислоты 2.4 г
Вода 46. 9 г

Витамины

Витамин A (A)0.45 мг
Витамин PP (PP)1.5 мг
Витамин A (РЭ) (A (РЭ))450 мкг
Витамин B1 (тиамин) (B1)0.55 мг
Витамин B2 (рибофлавин) (B2)0.42 мг
Витамин C (C)2.4 мг
Витамин E (ТЭ) (E (ТЭ))3 мг
Витамин PP (Ниациновый эквивалент) (PP)7.8 мг

Минеральные вещества

Железо (Fe)1.8 мг
Фтор (F)430 мкг
Молибден (Mo)4 мкг
Сера (S)315 мг
Фосфор (P)490 мг
Калий (K)90 мг
Натрий (Na)2284 мг
Магний (Mg)129 мг
Кальций (Ca)90 мг
—————————————-————-

Калорийность Рыбы нерка 157 кКал.

Энергетическая ценность продукта Рыба нерка (Соотношение белков, жиров, углеводов):

Белки: 20.3 г. (~81 кКал)
Жиры: 8.4 г. (~76 кКал)
Углеводы: 0 г. (~0 кКал)

Энергетическое соотношение (б|ж|у): 52%|48%|0%

Зола 1.2 г
Холестерин 60 мг
Насыщеные жирные кислоты 1.5 г
Вода 70.1 г

Витамины

Витамин PP (Ниациновый эквивалент) (PP)9. 5 мг
Витамин К (филлохинон) (K)0.3 мкг
Витамин E (ТЭ) (E (ТЭ))1.8 мг
Витамин D (D)11 мкг
Витамин C (C)1 мг
Витамин B12 (кобаламины) (B12)7.82 мкг
Витамин B9 (фолиевая кислота) (B9)11 мкг
Витамин B6 (пиридоксин) (B6)0.282 мг
Витамин B5 (пантотеновая кислота) (B5)1.14 мг
Витамин B2 (рибофлавин) (B2)0.15 мг
Витамин B1 (тиамин) (B1)0.2 мг
Витамин A (РЭ) (A (РЭ))50 мкг
Витамин A (A)0.05 мгВитамин PP (PP)5.7 мг

Минеральные вещества

Никель (Ni)6 мкг
Молибден (Mo)4 мкг
Фтор (F)430 мкг
Хром (Cr)55 мкг
Селен (Se)29.9 мкг
Марганец (Mn)0.014 мг
Медь (Cu)52 мкг
Цинк (Zn)0.7 мг
Железо (Fe)0.5 мг
Сера (S)203 мг
Хлор (Cl)165 мг
Фосфор (P)210 мг
Калий (K)390 мг
Натрий (Na)47 мг
Магний (Mg)24 мг
Кальций (Ca)7 мг

—————————————-—

неплохая инфа о кете : http://findfood.ru/product/krasnaja-ikra-kety
инфа о нерке : http://findfood. ru/product/ryba-nerka

Tags: Камчатка, икра

Антидепрессивный эффект кетамина опосредован энергетическим обменом и системой антиоксидантной защиты

1. Olesen J, et al. Консенсусный документ по европейским исследованиям мозга. J Neurol Нейрохирург Психиатрия. 2006; 77 (Приложение 1): i1–49. [Бесплатная статья PMC] [PubMed] [Google Scholar]

2. Murray CJ, Lopez AD. Альтернативные прогнозы смертности и инвалидности по причинам на 1990-2020 гг.: Исследование глобального бремени болезней. Ланцет. 1997; 349: 1498–1504. doi: 10.1016/S0140-6736(96)07492-2. [PubMed] [CrossRef] [Академия Google]

3. Agid Y, et al. Как можно улучшить поиск лекарств для лечения психических расстройств? Nat Rev Drug Discov. 2007; 6: 189–201. doi: 10.1038/nrd2217. [PubMed] [CrossRef] [Google Scholar]

4. Kessler RC, et al. Глобальное бремя психических расстройств: обновленная информация из обследований ВОЗ в области психического здоровья (WMH). Эпидемиол Психиатр Соц. 2009; 18:23–33. doi: 10.1017/S1121189X00001421. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

5. Kessler RC. Эпидемиология женщин и депрессии. J Аффективное расстройство. 2003; 74: 5–13. doi: 10.1016/S0165-0327(02)00426-3. [PubMed] [CrossRef] [Академия Google]

6. Организация, WH Depression. (2016).

7. Trivedi MH, et al. Оценка исходов циталопрама при депрессии с использованием лечения на основе измерений в STAR*D: значение для клинической практики. Am J Психиатрия. 2006; 163:28–40. doi: 10.1176/appi.ajp.163.1.28. [PubMed] [CrossRef] [Google Scholar]

8. Sonnenberg CM, Deeg DJ, Comijs HC, van Tilburg W, Beekman AT. Тенденции использования антидепрессантов пожилым населением: результаты исследования LASA за период в 10 лет. J Аффективное расстройство. 2008;111:299–305. doi: 10.1016/j.jad.2008.03.009. [PubMed] [CrossRef] [Google Scholar]

9. Раканьи Г., Пополи М. Клеточные и молекулярные механизмы длительного действия антидепрессантов. Диалоги Clin Neurosci. 2008; 10: 385–400. [Бесплатная статья PMC] [PubMed] [Google Scholar]

10. Kessler RC, et al. Эпидемиология большого депрессивного расстройства: результаты репликации национального обследования сопутствующих заболеваний (NCS-R) JAMA. 2003; 289:3095–3105. doi: 10.1001/jama.289.23.3095. [PubMed] [CrossRef] [Академия Google]

11. Берман Р.М. и соавт. Антидепрессивные эффекты кетамина у пациентов с депрессией. Биол психиатрия. 2000;47:351–354. doi: 10.1016/S0006-3223(99)00230-9. [PubMed] [CrossRef] [Google Scholar]

12. Хирота К., Ламберт Д.Г. Кетамин: его механизм(ы) действия и необычное клиническое применение. Бр Джей Анаст. 1996; 77: 441–444. doi: 10.1093/bja/77.4.441. [PubMed] [CrossRef] [Google Scholar]

13. Krystal JH, et al. Агонисты и антагонисты NMDA как зонды глутаматергической дисфункции и фармакотерапия при нервно-психических расстройствах. Харв Рев Психиатрия. 1999;7:125–143. doi: 10.3109/hrp.7.3.125. [PubMed] [CrossRef] [Google Scholar]

14. Krystal JH, et al. Системы глутамата и ГАМК как мишени для новых антидепрессантов и средств, стабилизирующих настроение. Мол Психиатрия. 2002; 7 (Приложение 1): S71–80. doi: 10.1038/sj.mp.4001021. [PubMed] [CrossRef] [Google Scholar]

15. Krystal JH, Sanacora G, Duman RS. Быстродействующие глутаматергические антидепрессанты: путь к кетамину и дальше. Биол психиатрия. 2013;73:1133–1141. doi: 10.1016/j.biopsych.2013.03.026. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

16. Kashiwagi K, et al. Блокаторы каналов, действующие на рецепторы N-метил-D-аспартата: дифференциальные эффекты мутаций в преддверии и порах ионных каналов. Мол Фармакол. 2002; 61: 533–545. doi: 10.1124/мол.61.3.533. [PubMed] [CrossRef] [Google Scholar]

17. Kotermanski SE, Johnson JW. Mg2+ придает селективность в отношении подтипа рецептора NMDA препарату для лечения болезни Альцгеймера мемантину. Дж. Нейроски. 2009; 29: 2774–2779. doi: 10.1523/JNEUROSCI.3703-08.2009. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

18. aan het Rot M, et al. Безопасность и эффективность многократного внутривенного введения кетамина при резистентной к лечению депрессии. Биол психиатрия. 2010;67:139–145. doi: 10.1016/j.biopsych.2009.08.038. [PubMed] [CrossRef] [Google Scholar]

19. Diazgranados N, et al. Рандомизированное дополнительное исследование антагониста N-метил-D-аспартата при резистентной к лечению биполярной депрессии. Арх генерал психиатрия. 2010; 67: 793–802. doi: 10.1001/archgenpsychiatry.2010.90. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

20. Ларкин Г.Л., Ботре А.Л. Предварительное натуралистическое исследование низких доз кетамина при депрессии и суицидальных мыслях в отделении неотложной помощи. Int J Neuropsychopharmacol. 2011;14:1127–1131. doi: 10.1017/S1461145711000629. [PubMed] [CrossRef] [Google Scholar]

21. Чаттерджи М., Гангули С., Сривастава М., Палит Г. Влияние «хронического» и «острого» введения кетамина и его эффект «отмены» на поведенческие изменения у мышей: последствия для экспериментального психоза. Поведение мозга Res. 2011; 216: 247–254. doi: 10.1016/j.bbr.2010.08.001. [PubMed] [CrossRef] [Академия Google]

22. Чаттерджи М., Верма Р., Гангули С., Палит Г. Нейрохимическая и молекулярная характеристика модели экспериментального психоза, вызванного кетамином, у мышей. Нейрофармакология. 2012;63:1161–1171. doi: 10.1016/j.neuropharm.2012.05.041. [PubMed] [CrossRef] [Google Scholar]

23. Swerdlow NR, Taaid N, Oostwegel JL, Randolph E, Geyer MA. На пути к межвидовой фармакологии сенсомоторного стробирования: влияние амантадина, бромокриптина, перголида и ропинирола на преимпульсное ингибирование акустического испуга у крыс. Бихав Фармакол. 1998;9:389–396. doi: 10.1097/00008877-199809000-00002. [PubMed] [CrossRef] [Google Scholar]

24. Cilia J, Hatcher P, Reavill C, Jones DN. (+/-) Вызванный кетамином дефицит ингибирования преимпульса акустической реакции вздрагивания у крыс не устраняется нейролептиками. Дж Психофармакол. 2007; 21: 302–311. doi: 10.1177/0269881107077718. [PubMed] [CrossRef] [Google Scholar]

25. Javitt DC, Zukin SR. Последние достижения в фенциклидиновой модели шизофрении. Am J Психиатрия. 1991; 148:1301–1308. doi: 10.1176/ajp.148.10.1301. [PubMed] [CrossRef] [Академия Google]

26. Li N, et al. Зависимое от mTOR образование синапсов лежит в основе быстрого антидепрессивного действия антагонистов NMDA. Наука. 2010; 329: 959–964. doi: 10.1126/science.11

. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

27. Zanos P, et al. Независимое от ингибирования NMDAR антидепрессивное действие метаболитов кетамина. Природа. 2016; 533:481–486. doi: 10.1038/nature17998. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

28. Weckmann K, Labermaier C, Asara JM, Müller MB, Turck CW. Зависимое от времени метаболическое профилирование действия препарата кетамина выявляет изменения пути гиппокампа и кандидатов в биомаркеры. Трансл Психиатрия. 2014;4:e481. doi: 10.1038/tp.2014.119. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

29. Джереми М. Берг, JLT и Люберт Страйер. Биохимия . 5-е издание . (2002).

30. Amodeo GA, Rudolph MJ, Tong L. Кристаллическая структура ядра гетеротримера Saccharomyces cerevisiae AMPK гомолога SNF1. Природа. 2007; 449: 492–495. doi: 10.1038/nature06127. [PubMed] [CrossRef] [Google Scholar]

31. Corton JM, Gillespie JG, Hawley SA, Hardie DG. 5-аминоимидазол-4-карбоксамид рибонуклеозид. Специфический метод активации АМФ-активируемой протеинкиназы в интактных клетках? Евр Дж Биохим. 1995;229:558–565. doi: 10.1111/j.1432-1033.1995.tb20498.x. [PubMed] [CrossRef] [Google Scholar]

32. Таунли Р., Шапиро Л. Кристаллические структуры аденилатного сенсора из АМФ-активируемой протеинкиназы делящихся дрожжей. Наука. 2007; 315:1726–1729. doi: 10.1126/science.1137503. [PubMed] [CrossRef] [Google Scholar]

33. Xiao B, et al. Структурная основа связывания AMP с AMP-активируемой протеинкиназой млекопитающих. Природа. 2007; 449: 496–500. doi: 10.1038/nature06161. [PubMed] [CrossRef] [Академия Google]

34. Xiao B, et al. Структура AMPK млекопитающих и ее регуляция с помощью АДФ. Природа. 2011; 472: 230–233. doi: 10.1038/nature09932. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

35. Xiao B, et al. Структурные основы регуляции AMPK низкомолекулярными активаторами. Нац коммун. 2013;4:3017. [Бесплатная статья PMC] [PubMed] [Google Scholar]

36. Barnes K, et al. Активация GLUT1 метаболическим и осмотическим стрессом: возможное участие AMP-активируемой протеинкиназы (AMPK) J Cell Sci. 2002; 115:2433–2442. [PubMed] [Академия Google]

37. Лущак В.И. Свободные радикалы, активные формы кислорода, окислительные стрессы и их классификация. Укр Биохим Ж. 2015;87:11–18. doi: 10.15407/ubj87.06.011. [PubMed] [CrossRef] [Google Scholar]

38. Ruszkiewicz J, Albrecht J. Изменения в митохондриальных антиоксидантных системах при нейродегенеративных заболеваниях и острых заболеваниях головного мозга. Нейрохим Инт. 2015; 88: 66–72. doi: 10.1016/j.neuint.2014.12.012. [PubMed] [CrossRef] [Google Scholar]

39. Begara-Morales JC, et al. Антиоксидантные системы регулируются посттрансляционными модификациями, опосредованными оксидом азота (NO-PTM) Front Plant Sci. 2016;7:152. дои: 10.3389/fpls.2016.00152. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

40. Wang, X. & Hai, C. Новое понимание окислительно-восстановительной системы и механизма окислительно-восстановительной регуляции. Mol Biol Rep , 10.1007/s11033-016-4022-y (2016). [PubMed]

41. Ри С.Г. Обзор пероксиредоксина. Мол клетки. 2016; 39:1–5. doi: 10.14348/molcells.2016.2368. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

42. Petersen AK, et al. О безгипотезном тестировании соотношений метаболитов в полногеномных и метаболомных ассоциативных исследованиях. Биоинформатика BMC. 2012;13:120. дои: 10.1186/1471-2105-13-120. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

43. Webhofer C, et al. Протеомное и метаболомное профилирование выявляет зависящие от времени изменения в метаболизме гиппокампа при лечении пароксетином и биомаркеры-кандидаты. J Psychiatr Res. 2013; 47: 289–298. doi: 10.1016/j.jpsychires.2012.11.003. [PubMed] [CrossRef] [Google Scholar]

44. Filiou MD, et al. Анализ протеомики и метаболомики мышиной модели тревожности по признаку выявляет расходящиеся митохондриальные пути. Биол психиатрия. 2011;70:1074–1082. doi: 10.1016/j.biopsych.2011.06.009. [PubMed] [CrossRef] [Google Scholar]

45. Scaini G, et al. Оценка ферментов цикла Кребса в головном мозге крыс после хронического введения антидепрессантов. Мозг Рес Бык. 2010; 82: 224–227. doi: 10.1016/j.brainresbull.2010.03.006. [PubMed] [CrossRef] [Google Scholar]

46. Magistretti PJ, Pellerin L, Rothman DL, Shulman RG. Энергия по запросу. Наука. 1999; 283:496–497. doi: 10.1126/science.283.5401.496. [PubMed] [CrossRef] [Google Scholar]

47. Webhofer C, et al. Метаболитный профиль действия антидепрессантов выявляет новые мишени для препаратов, помимо повышения уровня моноаминов. Трансл Психиатрия. 2011;1:e58. doi: 10.1038/tp.2011.56. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

48. Гланси Б., Балабан Р.С. Роль митохондриального Ca2+ в регуляции клеточной энергетики. Биохимия. 2012;51:2959–2973. doi: 10.1021/bi2018909. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

49. Chowdhury GM, et al. Кратковременно повышенный цикл глутамата в префронтальной коре крыс связан с быстрым появлением антидепрессантоподобных эффектов. Мол Психиатрия. 2017;22:120–126. doi: 10.1038/mp.2016.34. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

50. Karabatsiakis A, et al. Митохондриальное дыхание в мононуклеарных клетках периферической крови коррелирует с депрессивными субсимптомами и тяжестью большой депрессии. Трансл Психиатрия. 2014;4:e397. doi: 10.1038/tp.2014.44. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

51. Энглин, Р. Э., Роузбуш, П. И. и Мазурек, М. Ф. Лечение психических заболеваний у пациентов с митохондриальными расстройствами. Психосоматика с 51 , 179; ответ автора 179–180, 10.1176/appi.psy.51.2.179 (2010). [PubMed]

52. Anglin RE, Garside SL, Tarnopolsky MA, Mazurek MF, Rosebush PI. Психиатрические проявления митохондриальных расстройств: случай и обзор литературы. Дж. Клин Психиатрия. 2012; 73: 506–512. doi: 10.4088/JCP.11r07237. [PubMed] [CrossRef] [Академия Google]

53. Англин Р.Э., Тарнопольский М.А., Мазурек М.Ф., Роузбуш П.И. Психиатрические проявления митохондриальных нарушений у взрослых. J Нейропсихиатрия Clin Neurosci. 2012; 24:394–409. doi: 10.1176/appi.neuropsych.11110345. [PubMed] [CrossRef] [Google Scholar]

54. Мур С.М., Кристенсен Д.Д., Лафер Б., Фава М., Реншоу П.Ф. Более низкие уровни нуклеозидтрифосфата в базальных ганглиях пациентов с депрессией: исследование магнитно-резонансной спектроскопии фосфора-31. Am J Психиатрия. 1997; 154: 116–118. doi: 10.1176/ajp.154.1.116. [PubMed] [CrossRef] [Академия Google]

55. Volz HP, et al. Магнитно-резонансная спектроскопия 31P в лобной доле пациентов с глубокой депрессией. Eur Arch Psychiatry Clin Neurosci. 1998; 248: 289–295. doi: 10.1007/s004060050052. [PubMed] [CrossRef] [Google Scholar]

56. Cunningham JT, et al. mTOR контролирует окислительную функцию митохондрий посредством транскрипционного комплекса YY1-PGC-1alpha. Природа. 2007; 450:736–740. doi: 10.1038/nature06322. [PubMed] [CrossRef] [Google Scholar]

57. Morita M, et al. mTORC1 контролирует митохондриальную активность и биогенез посредством 4E-BP-зависимой регуляции трансляции. Клеточный метаб. 2013;18:698–711. doi: 10.1016/j.cmet.2013.10.001. [PubMed] [CrossRef] [Google Scholar]

58. Раманатан А., Шрайбер С.Л. Прямой контроль митохондриальной функции с помощью mTOR. Proc Natl Acad Sci USA. 2009;106:22229–22232. doi: 10.1073/pnas.0912074106. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

59. Coux O, Tanaka K, Goldberg AL. Структура и функции протеасом 20S и 26S. Анну Рев Биохим. 1996; 65: 801–847. doi: 10.1146/annurev.bi.65.070196.004101. [PubMed] [CrossRef] [Академия Google]

60. Кастл М., Грун Т. Окислительная модификация белков в стареющем организме и роль убиквитиновой протеасомной системы. Курр Фарм Дез. 2011;17:4007–4022. doi: 10.2174/138161211798764898. [PubMed] [CrossRef] [Google Scholar]

61. Gutteridge A, et al. Питательный контроль роста клеток эукариот: исследование системной биологии дрожжей. БМС Биол. 2010;8:68. дои: 10.1186/1741-7007-8-68. [Статья бесплатно PMC] [PubMed] [CrossRef] [Google Scholar]

62. Марондедзе С., Гроен А.Дж., Томас Л., Лилли К.С., Геринг С. Количественный фосфопротеомный анализ цГМФ-зависимых клеточных ответов у Arabidopsis thaliana. Мол завод. 2016;9: 621–623. doi: 10.1016/j.molp.2015.11.007. [PubMed] [CrossRef] [Google Scholar]

63. Юань М., Брайткопф С.Б., Ян Х., Асара Дж.М. Метаболомическая платформа с переключением положительных/отрицательных ионов на основе целевой масс-спектрометрии для биологических жидкостей, клеток, свежих и фиксированных тканей. Нат Проток. 2012; 7: 872–881. doi: 10.1038/nprot.2012.024. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

64. Xia J, Psychogios N, Young N, Wishart DS. MetaboAnalyst: веб-сервер для анализа и интерпретации метаболомных данных. Нуклеиновые Кислоты Res. 2009 г.;37:W652–660. doi: 10.1093/nar/gkp356. [PMC free article] [PubMed] [CrossRef] [Google Scholar]

65. Тушер В.Г., Тибширани Р., Чу Г. Анализ значимости микрочипов применительно к реакции на ионизирующее излучение. Proc Natl Acad Sci USA. 2001; 98: 5116–5121. doi: 10.1073/pnas.091062498. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

66. Сванте В., Майкл С., Леннарт Э. В хемометрике и интеллектуальных лабораторных системах. 2001; 58: 109–130. doi: 10.1016/S0169-7439(01)00155-1. [Перекрестная ссылка] [Академия Google]

67. Хосак Д.А., Деннис Г., Шерман Б.Т., Лейн Х.К., Лемпицки Р.А. Идентификация биологических тем в списках генов с помощью EASE. Геном биол. 2003;4:R70. doi: 10. 1186/gb-2003-4-10-r70. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

68. Szklarczyk D, et al. База данных STRING в 2017 году: широкодоступные сети межбелковых ассоциаций с контролируемым качеством. Нуклеиновые Кислоты Res. 2017; 45:D362–D368. doi: 10.1093/nar/gkw937. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

13: Элементы обозначения Дирака

1. Последнее обновление

2. Сохранить как PDF

• Франк Риу
• Колледж Святого Бенедикта/Университет Святого Иоанна

На заре квантовой теории П.А.М. (Поль Адриан Морис) Дирак создал для нее мощный и лаконичный формализм, который сейчас называется нотацией Дирака или скобкой (скобка \( \langle \, | \, \rangle\ )) обозначение.

В квантовой механике возникли две основные математические традиции: матричная механика Гейзенберга и волновая механика Шрёдингера . Эти совершенно разные вычислительные подходы к квантовой теории формально эквивалентны, каждый со своими сильными сторонами в определенных приложениях. Вариант Гейзенберга, как следует из его названия, основан на матричной и векторной алгебре, в то время как подход Шредингера требует интегрального и дифференциального исчисления. Обозначение Дирака можно использовать на первом этапе, когда описывается или настраивается квантово-механический расчет. После этого для завершения расчета выбирают либо матричную, либо волновую механику, в зависимости от того, какой метод является наиболее целесообразным в вычислительном отношении.

Кет

В обозначениях Дирака известное помещается в кет, \(| \, \rangle\). Так, например, \(| p \rangle\) выражает тот факт, что частица имеет импульс \(p\). Это могло бы быть и более явным: \(| p=2 \rangle\), частица имеет импульс, равный 2; \(| x=1. 2\), представляет собой плотность вероятности того, что частица в состоянии \( \psi \) будет найдена при \(х\) = 0,25. Таким образом, мы видим, что пара скобка-кет может представлять собой событие, результат эксперимента. В квантовой механике эксперимент состоит из двух последовательных наблюдений — одного, устанавливающего начальное состояние (кет), и другого, устанавливающего конечное состояние (бюстгальтер).

Пары Бра-Кет

Если мы пишем \( \langle x| \psi \rangle \), мы выражаем \( \psi \) в координатном пространстве, не указывая явно фактическое значение \(x\). \(\langle 0.25 | \psi \rangle \) является числом , но более общее выражение \(\rangle x | \psi \rangle \) является математической функцией, математической функцией \(x\), или мы могли бы сказать математический алгоритм для генерации всех возможных значений \( \langle x| \psi \rangle \), амплитуды вероятности того, что система в состоянии \( | \psi \rangle \) имеет положение \(x\) . 92} \]

Как найти это последнее выражение, мы обсудим позже.

Важным моментом здесь является то, что существует более одного языка для выражения \( | \psi \rangle \). Наиболее распространенным языком для химиков является координатное пространство (\(x\), \(y\) и \(z\), или \(r\), \(\theta\) и \(\phi\) и т. д.), но мы увидим, что импульсное пространство предлагает столь же важный взгляд на функцию состояния. Важно признать, что \( \langle x| \psi \rangle \) и \( \langle p| \psi \rangle \) формально эквивалентны и содержат одну и ту же физическую информацию о состоянии системы. Один из постулатов квантовой механики состоит в том, что если вы знаете \( | \psi \rangle \), вы знаете все, что нужно знать о системе, и если, в частности, вы знаете \( \langle x| \psi \ rangle \), вы можете вычислить все свойства системы и преобразовать \( \langle x| \psi \rangle \), если хотите, в любой другой подходящий язык, например импульсное пространство.

Пара бра-кет также может рассматриваться как векторная проекция (то есть скалярное произведение) — проекция содержимого кет на содержимое лифчика или «тень», которую кет отбрасывает на бюстгальтер . Например, \( \langle \Phi | \psi \rangle \) — это проекция состояния \(\psi\) на состояние \(\Phi\). Это амплитуда (амплитуда вероятности) того, что система в состоянии \( | \psi \rangle \) впоследствии окажется в состоянии \(| \Phi \rangle \). Это также то, что мы стали называть интегралом перекрытия 9 .2\), действительное число.

Линейная суперпозиция

К приведенному выше анализу можно подойти менее прямым, но все же показательным способом, записав \(| \psi \rangle\) и \( \langle \Phi |\) как линейные суперпозиции в собственных состояниях оператор положения, как показано ниже.

\[ | \psi \rangle = \int | х \рангл \лангл х | \psi \rangle \, dx \]

\[ \langle \Phi | = \int \langle \Phi | x’ \rangle \langle x’ | \, dx’ \]

Объединение их в виде пары скобок дает

\[ \langle \Phi | \psi \rangle = \iint \langle \Phi | x’ \rangle \langle x’ | х \рангл \лангл х | \psi \угол \; dx’ \,dx = \int \langle \Phi | х \рангл \лангл х | \psi \угол \; dx\]

\(x’\) исчезает, потому что собственные состояния положения являются ортогональным базисом множества и \( \langle x’ | x \rangle =0 \), если \(x’ = x\), в котором случае оно равно 1.

\( | \psi \rangle = \sum_n | n \rangle \langle n | \psi \rangle\) является линейной суперпозицией в дискретном (а не непрерывном) базисном наборе \(\{| п\угол \}\). Конкретный пример такого типа суперпозиции легко продемонстрировать с помощью матричной механики.

Нельзя слишком сильно подчеркнуть, что линейная суперпозиция — это , а не смесь. Например, когда система находится в состоянии \( | S_{su} \rangle \) каждое измерение спина в направлении \(x\) дает один и тот же результат: спин вверх . Однако измерение вращения в направлении z дает вращение вверх в 50% случаев и вращение вниз в 50% случаев. Система имеет четко определенное значение вращения в направлении x, но неопределенное значение вращения в направлении z. Легко вычислить вероятности для измерений спина в направлении z: 93)\]

Поскольку собственные функции для задачи о частице в коробке образуют полный базисный набор , \(\Phi(x)\) можно записать в виде линейной комбинации (т. е. линейной суперпозиции) этих собственных функций.

\[ | \Phi \rangle = \sum_n |n \rangle \langle n| \Phi \rangle = \sum_n | n \rangle \int \langle n |x \rangle \langle x | \Phi \rangle dx\]

В этих обозначениях \(\langle n | \Phi \rangle \) является проекцией \(| \Phi \rangle \) на собственное состояние \(|n\rangle\). Эта проекция или тень \(\Phi\) на \(n\) может быть записана как \(c_n\). Это мера вклада \(| n \rangle \)) в состояние \(| \Phi \rangle \). Это также интеграл перекрытия. Поэтому мы можем написать

\[ | \Phi \rangle = \sum_n | n \rangle c_n \]

Используя численное программное обеспечение, такое как Matlab, легко показать, что первые десять коэффициентов в этом разложении равны:

Эти коэффициенты разложения доказывают, что волновая функция следа сильно напоминает собственное состояние с самой низкой энергией (\(|n \rangle \)) частицы в системе ящиков.

Операторы, собственные векторы, собственные значения и математические ожидания

В матричной механике операторы представляют собой матрицы, а состояния представлены векторами. Матрицы оперируют векторами, чтобы получить полезную физическую информацию о состоянии системы. Согласно квантовой теории, для каждой физической наблюдаемой есть оператор, и система либо находится в состоянии с четко определенным значением этой наблюдаемой, либо нет. Операторы, связанные со спином в направлениях \(x\) и \(z\), показаны ниже в единицах по 9.0003

При выполнении операций результат S является собственной функцией или собственным вектором с собственным значением 1 (в единицах h/4). Однако Sxu не является собственной функцией, потому что где Это означает, как упоминалось в предыдущем разделе, что S не имеет определенного значения для спина в направлении z. В этих обстоятельствах мы не можем с уверенностью предсказать результат измерения спина в направлении z, но мы можем вычислить среднее значение для большого количества измерений. Это называется ожидаемым значением 9.0112 и в обозначениях Дирака представляется следующим образом: В матричной механике вычисляется следующим образом.

Этот результат согласуется с предыдущим обсуждением, которое показало, что это линейная суперпозиция 50-50 и с собственными значениями +1 и -1 соответственно. Другими словами, в половине случаев результат измерения равен +1, а в другой половине -1, что дает среднее значение, равное нулю. Теперь мы рассмотрим вычисление ожидаемого значения для системы в состоянии , которое настроено следующим образом: Чтобы сделать это вычисление удобным для вычислений, мы расширим собственные состояния оператора положения. Обратите внимание на упрощение, которое происходит, потому что

Вариационный метод

Мы предварительно рассмотрели вариационный метод, приближенный метод, используемый, когда точное решение уравнения Шредингера недоступно. Используя

\[ \Phi(x) = \sqrt{30} x (1 -x)\]

в качестве пробной волновой функции для задачи о частице в ящике, мы оцениваем среднее значение энергии как

\[ \langle E \rangle = \langle \Phi | \шляпа{Н} | \Phi \rangle \]

Однако, используя формализм Дирака, мы можем разложить \(\Phi\), как отмечалось выше, по собственным функциям \(H\) следующим образом. 2E_n\] 92\) 0,9987 0,0014, 0,00006 0,00001

Все остальные коэффициенты равны нулю или исчезающе малы. Эти результаты говорят о том, что если мы произведем измерение энергии системы в состоянии, представленном буквой М, то с вероятностью 99,87 % мы получим 4,935, с вероятностью 0,14 % мы получим 19,739 и так далее. Тогда мы могли бы сказать, что состояние \(\Phi\) является линейной комбинацией первых четырех нечетных собственных функций, причем первая собственная функция вносит наибольший вклад.

Вариационная теорема утверждает, что, как бы вы ни старались построить пробные волновые функции, вы не сможете добиться большего, чем «истинное» значение энергии основного состояния, и это уравнение улавливает этот важный принцип. Единственный способ, которым M может дать правильный результат для основного состояния частицы в ящике, например, если \(c_1 = 1\) или если \(M\) является самой собственной функцией.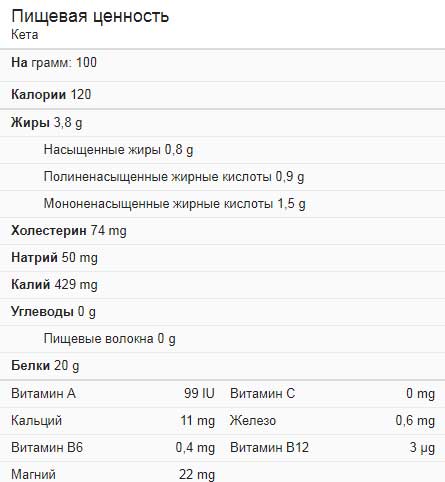 Если это не так, то с < 1, а остальные значения с отличны от нуля, и энергия должна быть больше \(Е\). Еще раз взглянув на последние два уравнения, мы увидим, что оператор измерения всегда можно записать как оператор проектирования, включающий его собственные состояния.

Оператор импульса в координатном пространстве

Корпускулярно-волновой дуализм лежит в основе квантовой механики. Частица с длиной волны имеет волновую функцию (ненормализованную). Однако согласно волновому уравнению де Бройля e импульс частицы равен . Поэтому волновая функция импульса частицы в координатном пространстве равна . В импульсном пространстве имеет место следующее уравнение на собственные значения: . Работа с собственной функцией импульса с оператором импульса в импульсном пространстве возвращает собственное значение импульса, умноженное на исходную собственную функцию импульса. Другими словами, в своем собственном пространстве оператор импульса является мультипликативным оператором (то же верно и для оператора положения в координатном пространстве). Чтобы получить оператор импульса в координатном пространстве, это выражение можно спроецировать на координатное пространство, действуя слева с помощью .

Сравнение первого и последнего членов показывает, что это и есть оператор импульса в координатном пространстве. волновая функция положения в импульсном пространстве. Используя описанный выше метод, легко показать, что позиционный оператор в импульсном пространстве имеет вид распределяются в пространстве на атомы и молекулы. Однако квантовая механика имеет эквивалентную формулировку в импульсном пространстве. Он отвечает на вопрос, как выглядит распределение скоростей электронов? Обе формулировки эквивалентны, т. е. содержат одну и ту же информацию, и формально связаны преобразованием Фурье. Нотация Дирака очень ясно показывает эту связь.

\[p px x dx \psi= \psi\]

Начиная слева, у нас есть амплитуда, что система в состоянии Q имеет положение x. Тогда, если он имеет положение x, амплитуда импульса p. Затем мы суммируем все значения x, чтобы найти все способы, которыми система в состоянии Q может иметь импульс p. В качестве частного примера можно выбрать задачу о частице в ящике с указанными выше собственными функциями. Легко показать, что собственные состояния импульса в позиционном пространстве в атомных единицах (см. предыдущий раздел) равны . Это, конечно, означает, что комплексное сопряжение есть. Следовательно, преобразование Фурье Q(x) в импульсное пространство

Этот интеграл можно вычислить аналитически, и он дает следующие волновые функции импульсного пространства для частицы в ящике. Ниже показано графическое отображение функции распределения импульсов (p) для нескольких состояний.

Резюме и ссылки

Дж. Л. Мартин (см. ссылки ниже) определил четыре достоинства нотации Дирака.

1. Это лаконично. В нотации Дирака есть небольшое количество основных элементов: бюстгальтеры, кеты, пары бра-кет, произведения кет-бра и отношение полноты (непрерывное и дискретное). С помощью этих нескольких строительных блоков вы можете построить всю квантовую теорию.
2. Он гибкий. Вы можете использовать его, чтобы сказать одно и то же несколькими способами; легко переводить с одного языка на другой. Возможно, то понимание, которое нотация Дирака дает преобразованию Фурье, является лучшим примером этого достоинства.
3. Это вообще. Это синтаксис для описания того, что вы хотите сделать, не привязывая себя к конкретному вычислительному подходу. Другими словами, вы используете его для постановки задачи, а затем выбираете наиболее быстрый способ выполнения расчета.
4. Хотя это не совсем отраслевой стандарт, он должен быть им по причинам, перечисленным в пунктах 1-3 выше. Он широко используется, поэтому, если вы хотите читать литературу по квантовой химии и физике, вам необходимо изучить нотацию Дирака. Кроме того, он используется в большинстве лучших учебников по квантовой химии и физике.
5. Я хотел бы добавить пятую добродетель. Как только вы освоите его, вы обнаружите, что он прост в использовании и очень поучителен. Это облегчает понимание всех фундаментальных квантовых концепций.