Главная Школьные новости Фотогалерея Документы Для родителей Государственная Итоговая Аттестация Вопросы и ответы

Главная

Зачисление в ОУ

Официальный сайт

Прямая ссылка на наше учреждение

Форум Победителей РФ

Cat Vector Набор Векторов и Иллюстраций. Вектор кет

Квантовомеханические векторы и операторы в гильбертовом пространстве. I

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

Математический аппарат квантовой механики, как оказалось, имеет своим истоком обычную классическую реальность.

Поэтому проиллюстрируем прямо сейчас, не обращаясь к квантовой физике, его существенные черты.

1. Независимость описания реальности от выбора систем координат.

Физическая реальность, а именно, перемещение тел, действующие силы, напряжённости электрических и магнитных полей и т.п. существуют объективно, независимо от нас.

Мы можем произвольно выбирать системы координат и, в зависимости от нашего выбора, получаем разные формулы. Но за всеми различиями в формулах скрывается объективно существующая физическая реальность. Следовательно, возможно описание реальности свободное от произвола, обусловленного выбором систем координат, короче говоря, возможно инвариантное описание реальности.

Именно на этом основана векторная (и тензорная) алгебра, причём векторы являются объектами трёхмерного евклидового, а попросту говоря, физического пространства.

Но мы знаем (см. Описание направлений и поворотов в трёхмерном пространстве. III), что направления физического пространства можно задавать через математические объекты двумерного комплексного евклидового пространства. — В связи с этим открывается ещё одна возможность инвариантного описания физической реальности.

2. Кет- и бра- векторы.

Итак, пусть имеется единичный вектор, определяющий направление какой-либо физической величины, — силы, вектора напряжённости поля, оси вращения и т.п. Этому вектору соответствует в двумерном евклидовом пространстве вектор

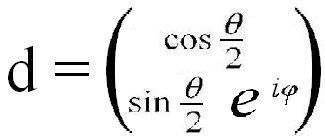такой, что d†d=1.

После умножения этого вектора на произвольное комплексное число с единичным модулем, матричные элементы матрицы d изменятся, но матрица d всё равно будет задавать то же самое направление (см. Описание направлений и поворотов в трёхмерном пространстве. III).

И ещё. Повернём систему координат произвольным образом. Матрицы поворота, как известно, таковы (см. Описание направлений и поворотов в трёхмерном пространстве. II):

UX(α/2) = Е cosα/2 + iσxsinα /2,

UY(α/2) = Е cosα/2 + iσysinα/2,

UZ(α/2) = Е cosα/2 + iσzsinα/2 .

В результате получим матрицу d′ = Ud, здесь U — или одна из матриц UX(α/2), UY(α/2), UZ(α/2), или их любое произведение.

И опять, несмотря на то, что d и d′ = Ud совершенно разные матрицы, они изображают одно и то же направление (пассивная интерпретация).

Поэтому возникает естественное желание изображать всевозможные матрицы, изображающие одно и то же направление, единообразно, т.е. инвариантно, например, так: |d›.

|d› называют кет-вектором.

Поскольку матрицам d соответствуют вполне определённые эрмитово сопряжённые матрицы d†, то введём обозначение |d›† = ‹d|.

Вектор ‹d| называют бра-вектором.

В результате двойного эрмитового сопряжения любая матрица возвращается к исходному виду. И поскольку инвариантными обозначениями зашифрованы обычные матрицы, то

‹d|† = (|d›†)† = |d›,

Теперь выражение d†d = 1 можно записать в инвариантной форме:

‹d|d› = 1.

Здесь и далее идёт речь о своеобразной модификации векторного исчисления, которая была разработана выдающимся английским физиком-теоретиком Полем Дираком специально для квантовой механики.

Выражение ‹d|d› является, по сути, скобкой. По-английски скобка — bracket. Отсюда понятно, почему векторы ‹d| и |d› называются бра-векторами и кет-векторами соответственно.

То, что ‹d|d› = 1 означает, что вектор |d› нормирован на единицу, иначе говоря, норма (длина) вектора d равна единице, r = 1.

Следует подчеркнуть, что только векторы, нормированные на единицу, изображают направления в трёхмерном евклидовом (физическом) пространстве.

Известно, что угол между двумя направлениями d1 и d2 вычисляется по формуле (см. Описание направлений и поворотов в трёхмерном пространстве. VI):

cos2α/2 = (d2†d1) · (d2†d1)* = |(d2†d1)|2.

В инвариантной форме формула принимает следующий вид:

cos2α/2 = ‹d2|d1›‹d2|d1›* = |‹d2|d1›|2.

3. Гильбертово пространство.

До сих пор мы воспринимали двумерное комплексное эвклидово пространство чисто интуитивно, — оно подобно двумерному действительному евклидовому пространству с единственным отличием: координаты, а также компоненты векторов могут быть комплексными числами.

Теперь определим это понятие более чётко.

Матрицу d можно представить в следующем виде:

d = (cosθ/2)е1 + (еiφ · sinθ/2)е2 ,

здесь

е1 и е2 обладают следующими свойствами: е1Т · е1 = е2Т · е2 = 1, е1Т · е2 = е2Т · е1 = 0, или, что то же самое,

еiТ · еj = δij , i, j = 1, 2.

Здесь δij— символ Кронекера. Он равен единице, если i = j и нулю, если i ≠ j.

Сейчас, пока мы рассматриваем самые простые ситуации, введение общепринятых компактных обозначений, вроде символа Кронекера, знака суммирования и т.п., кажется неуместным. Но уже теперь пора к ним привыкать, потому что общепринятые обозначения экономны, они позволяют обобщать многие результаты на более сложные случаи с минимальными усилиями, можно сказать, автоматически.

Теперь запишем d в инвариантной форме:

|d› = (cosθ/2)|е1› + ( еiφ · sinθ/2)|е2›,

причём

‹еi|еj› = δij, i, j = 1, 2.

Обратите внимание на то, что вектор |d› нормирован на единицу, ‹d|d›=1. Именно это условие должно выполняться для того, чтобы вектор |d› задавал какое-то направление в трёхмерном евклидовом пространстве.

Определение. Множество всех векторов типа

где b1 и b 2 — произвольные комплексные числа, называется двумерным комплексным евклидовым пространством. Его также называют гильбертовым пространством, потому что если размерность пространства конечная, то двумерное комплексное евклидово пространство и (комплексное) гильбертово пространство совпадают.

В дальнейшем будем применять термин «гильбертово пространство», потому что так короче.

Векторы |е1› и |е2› составляют ортонормированный базис гильбертова пространства. «Орто-» значит ортогональный, то есть ‹е1|е2› = ‹е2|е1› = 0, «нормированный» значит нормированный на единицу ‹е1|е1› = ‹е2|е2› = 1.

Теперь вычислим

‹е1|b› = ‹е1|(b 1|е1› + b2|е2›) = b1‹е1|е1› + b2‹е1|е2›) = b 1.

Аналогично вычисляется ‹е2|b› = b2.

Итак, коэффициенты разложения любого вектора по базисным векторам гильбертова пространства равны:

bk= ‹еk|b›, k = 1, 2.

Как мы уже знаем, для того чтобы вектор гильбертова пространства изображал какое-то направление трёхмерного евклидового пространства, необходимо, чтобы он был нормирован на единицу. Итак, потребуем, чтобы ‹b|b› = 1:

‹b|b› = (b1*‹е1| + b 2*‹е2|)(b1|е1› + b 2|е2›)=

b1*· b1‹е1|е1› + b 1*· b2‹е1|е2› + b2*· b1‹е2|е1› + b 2*· b 2‹е2|е2› =

b 1*· b 1 + b2* · b 2 = |b1|2 + |b 2|2 = 1,

т.е. условие нормировки любого вектора двумерного гильбертова пространства имеет вид:

Если у вас возникают сомнения в том, правильно ли выполняются инвариантные вычисления, то вспомните, что инвариантные обозначения возникли из матричного исчисления, поэтому для них справедливы все правила действий с матрицами.

Продолжение

vestishki.ru

вектор - это... Что такое Кет-вектор?

〈	∣	〉
bra		ket
бра		кет

Бра и кет (англ. bra-ket ← bracket скобка) — алгебраический формализм (система обозначений), предназначенный для описания квантовых состояний.

Называется также обозначениями Дирака. В матричной механике данная система обозначений является общепринятой.

Определение и использование

Квантовая система рассматривается в гильбертовом пространстве , элементы (векторы) которого обозначаются как «кет-векторы». Сопряжённое пространство , элементы которого обозначаются как «бра-векторы», совпадает с с точностью до комплексного сопряжения. Это означает, что каждому кет-вектору можно сопоставить бра-вектор , и обратно.

Скалярное произведение бра-вектора с кет-вектором записывается в виде ; две вертикальные черты «сливаются». Квадрат вектора, по определению гильбертова пространства, неотрицателен: . На вектора, описывающие состояния системы, накладывается условие нормировки .

Свёртка оператора А с бра-вектором и кет-вектором записывается как ; это также скаляр (комплексное число). В частности, матричный элемент оператора А в определённом базисе (в тензорных обозначениях — Akl) записывается в обозначениях Дирака как , а среднее значение наблюдаемой на состоянии ψ — как .

Умножение векторов на оператор (кет-вектора — слева, бра-вектора — справа) даёт векторы того же типа и записывается тем же способом, что принят в алгебре:

Например, уравнение Шрёдингера (для стационарного состояния) будет иметь вид:

, где H — гамильтониан, а E — скаляр (уровень энергии).

Отличия бра-кет-обозначений от традиционных

В математике употребляется обозначение «полуторалинейного» скалярного произведения в гильбертовом пространстве, имеющее тот же смысл, что и перемножение бра на кет. Однако, математики обычно рассматривают угловые скобки как знак операции, а не части обозначения вектора. Традиционное математическое обозначение, в отличие от дираковского, несимметрично — оба вектора предполагаются величинами одного типа, и по первому аргументу из двух операция является антилинейной. С другой стороны, произведение бра и кет является билинейным, но от двух аргументов разного типа. Сопряжённым к кет-вектору будет являться бра-вектор (где i — мнимая единица). Однако, в квантовой механике эту странность обозначений позволено игнорировать, поскольку квантовое состояние, представляемое вектором, не зависит от его умножения на любые комплексные числа, по модулю равные единице. Также, использование бра и кет позволяет подчеркнуть отличие состояния ψ (записывается без скобок и палок) от конкретных векторов, его представляющих.

В отличие от алгебраических обозначений, где элементы базиса обозначаются как ek, в бра-кет-обозначениях указывается только индекс базисного элемента: . Этим они похожи на тензорные обозначения, но в отличие от последних позволяют записывать произведения операторов с векторами без использования дополнительных (подстрочных или надстрочных) букв.

Математические свойства

Бра и кет можно использовать и в чистой математике для обозначения элементов сопряжённых друг другу линейных пространств. Кет-векторы считаются при этом «векторами-столбцами», а бра-векторы — «векторами-строками». Перемножение бра- и кет-векторов друг на друга и на операторы можно рассматривать как частный случай матричного формализма «строка на столбец». А именно, надо положить кет-векторы матрицами размера N×1, бра-векторы — размера 1×N, операторы — размера N×N, где N — количество состояний квантовой системы (размерность пространства ). Матрицы размера 1×1 имеют единственный элемент и отождествляются со скалярами. В случае бесконечномерного пространства состояний на «матрицы» (фактически, ряды) приходится накладывать дополнительные условия сходимости.

Формула для сопряжённого вектора выглядит следующим образом:

, где

Запись типа 〈 … 〉 всегда означает скаляр. Бра-вектор всегда имеет скобку 〈 слева, кет-вектор — скобку 〉 справа. Произведение в «неестественном» порядке — 〉 〈 — даёт так называемый кет-бра-оператор — оператор ранга 1, являющийся тензорным произведением и . Они часто рассматриваются в теории операторов и квантовых вычислениях. В частности, оператор (при нормировке ) является проектором на состояние ψ, точнее, на соответственное одномерное линейное подпространство в .

Имеет место ассоциативность:

и т.д.

Интересные факты

На семинаре в Институте физических проблем во время выступления Дирака, Ландау переводил термины "бра" и "кет" как "ско" и "бка".

Литература

Ю. М. Белоусов. Курс квантовой механики. Нерелятивистская теория. Москва. 2006.

Wikimedia Foundation. 2010.

dic.academic.ru

Cat Vector Фотографии, картинки, изображения и сток-фотография без роялти

#42305827 - cat set

Вектор

Похожие изображения

Добавить в Лайкбокс

#53513431 - Cute black vector cat icon isolated on white

Вектор

Похожие изображения

Добавить в Лайкбокс

#38634937 - CAT logo vector

Вектор

Похожие изображения

Добавить в Лайкбокс

#58537359 - Cat in sunglassesFunny summer hand drawing calligraphy, vector..

Вектор

Похожие изображения

Добавить в Лайкбокс

#29394439 - Cat color styled silhouette image Concept of animal pet, veterinary,..

Вектор

Похожие изображения

Добавить в Лайкбокс

#39199068 - Vector cat

Вектор

Похожие изображения

Добавить в Лайкбокс

#44724343 - Cartoon plump kitty, vector illustration of funny cute striped..

Вектор

Похожие изображения

Добавить в Лайкбокс

#35070594 - Cat Vector Set

Вектор

Похожие изображения

Добавить в Лайкбокс

#48208439 - Cats vector set

Вектор

Похожие изображения

Добавить в Лайкбокс

#47554961 - Cat pet animal holding clean welcome sweet home board vector..

Вектор

Похожие изображения

Добавить в Лайкбокс

#28961343 - Dog and cat set Collection of vector pets icon silhouette

Вектор

Похожие изображения

Добавить в Лайкбокс

#45588938 - cat set

Вектор

Похожие изображения

Добавить в Лайкбокс

#33223647 - Fashion portrait of hipster cat in glasses in the form of stars..

Вектор

Похожие изображения

Добавить в Лайкбокс

#43647116 - Vector image of a big set of cat icometric icons

Вектор

Похожие изображения

Добавить в Лайкбокс

#30451601 - Close-up portrait of hairless Sphinx cat on black background..

Вектор

Похожие изображения

Добавить в Лайкбокс

ru.123rf.com

вектор - Большая Энциклопедия Нефти и Газа, статья, страница 1

Кет-вектор

Cтраница 1

Кет-вектор 10) является вакуумным вектором, имеющим нулевой квант; см. разд. [1]

Кет-вектор /) представляет собой атомную волновую функцию в 1 - й ячейке решетки. [2]

Кет-вектор /) представляет собой атомную волновую функцию в / - Й ячейке решетки. [3]

Кет-вектор ost обозначает присутствие фотона с частотой as, a 0 /) означает, что этот фотон был уничтожен. [4]

Обозначим кет-векторы одного изу - мультиплетов, рассмотренных в последнем разделе, через I ( j j) jm) ( см. примечание на стр. [5]

Каждый кет-вектор а) имеет соответствующий бра-вектор ( а; любые числа, появляющиеся в бра-векторе, комплексно сопряжены с числами, входящими в соответствующий кет-вектор. [6]

Рассмотрим произвольный кет-вектор т), описывающий одно из возможных состояний нашей системы. [7]

Соответственно кет-векторы сложной системы являются произведениями кет-векторов отдельных частиц. [8]

Бра - и кет-векторы находятся во взаимно однозначном соответствии. Тем не менее, нужно их как-то различать - именно для этого и были введены угловые скобки. [9]

В таком случае собственные кет-векторы оператора Н являются одновременно и собственными кет-векторами оператора Н, а собственные значения Н отличаются от собственных значений Н в ( 2т) - 1 раз. [10]

Здесь под обозначением кет-вектора х) понимается, что х есть ( чистое) квантовое состояние. Гильбертово пространство, ассоциируемое с нашей квантовой системой, является комплексным векторным пространством с базисом из 2 векторов, и состояние нашей системы в любой момент времени представлено вектором единичной длины этого гильбертова пространства. Поскольку умножение этого вектора-состояния на фазовый множитель единичной длины не изменяет состояние системы, нам достаточно только 2 - 1 комплексных чисел для полного описания этого состояния. [11]

Для определения длины кет-векторов необходима какая-то аналогичная процедура. [12]

Собственные бра - и кет-векторы динамического оператора образуют таким образом ортогональную систему, аналогичную ортогональному набору векторов. Если это произведение равно единице, говорят, что бра - и кет-векторы нормированы. В дальнейшем будем считать, что собственные бра - и кет-векторы динамического оператора нормированы, если только нет специальных оговорок. [13]

Произведение бра - и кет-векторов ( и у) является скаляром; произведение кет - и бра-векторов у ( и, как можно показать, будет оператором. [14]

Произведение бра - и кет-векторов ( и у является скаляром; произведение кет - и бра-векторов / ( (, как можно показать, будет оператором. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

ket vector — с английского на русский

ket vector — ket vektorius statusas T sritis fizika atitikmenys: angl. ket vector vok. ket Vektor, m rus. кэт вектор, m pranc. vecteur de ket, m … Fizikos terminų žodynas

ket vektorius — statusas T sritis fizika atitikmenys: angl. ket vector vok. ket Vektor, m rus. кэт вектор, m pranc. vecteur de ket, m … Fizikos terminų žodynas

ket-Vektor — ket vektorius statusas T sritis fizika atitikmenys: angl. ket vector vok. ket Vektor, m rus. кэт вектор, m pranc. vecteur de ket, m … Fizikos terminų žodynas

ket — noun /kɛt/ a) A vector, in Hilbert space, especially as representing the state of a quantum mechanical system; the complex conjugate of a bra; a ket vector. Symbolised by |&GT;. b) Carrion; any filth … Wiktionary

Vector propio y valor propio — Fig. 1. En esta transformación de la Mona Lisa, la imagen se ha deformado de tal forma que su eje vertical no ha cambiado. (nota: se han recortado las esquinas en la imagen de la derecha) … Wikipedia Español

vecteur de ket — ket vektorius statusas T sritis fizika atitikmenys: angl. ket vector vok. ket Vektor, m rus. кэт вектор, m pranc. vecteur de ket, m … Fizikos terminų žodynas

Complex conjugate vector space — In mathematics, the (formal) complex conjugate of a complex vector space is the complex vector space consisting of all formal complex conjugates of elements of . That is, is a vector space whose elements are in one to one correspondence with the… … Wikipedia

Bra-ket notation — Quantum mechanics Uncertainty principle … Wikipedia

Notación Bra-Ket — La notación bra ket,[1] [2] también conocida como notación de Dirac por su inventor Paul Dirac, es la notación estándar para describir los estados cuánticos en la teoría de la mecánica cuántica. Puede también ser utilizada para denotar vectores… … Wikipedia Español

кэт-вектор — ket vektorius statusas T sritis fizika atitikmenys: angl. ket vector vok. ket Vektor, m rus. кэт вектор, m pranc. vecteur de ket, m … Fizikos terminų žodynas

Quantum state — In quantum physics, a quantum state is a mathematical object that fully describes a quantum system. One typically imagines some experimental apparatus and procedure which prepares this quantum state; the mathematical object then reflects the… … Wikipedia

translate.academic.ru

Vector Cat Фотографии, картинки, изображения и сток-фотография без роялти

#42305827 - cat set

Вектор

Похожие изображения

Добавить в Лайкбокс

#53513431 - Cute black vector cat icon isolated on white

Вектор

Похожие изображения

Добавить в Лайкбокс

#38634937 - CAT logo vector

Вектор

Похожие изображения

Добавить в Лайкбокс

#58537359 - Cat in sunglassesFunny summer hand drawing calligraphy, vector..

Вектор

Похожие изображения

Добавить в Лайкбокс

#29394439 - Cat color styled silhouette image Concept of animal pet, veterinary,..

Вектор

Похожие изображения

Добавить в Лайкбокс

#39199068 - Vector cat

Вектор

Похожие изображения

Добавить в Лайкбокс

#44724343 - Cartoon plump kitty, vector illustration of funny cute striped..

Вектор

Похожие изображения

Добавить в Лайкбокс

#35070594 - Cat Vector Set

Вектор

Похожие изображения

Добавить в Лайкбокс

#48208439 - Cats vector set

Вектор

Похожие изображения

Добавить в Лайкбокс

#47554961 - Cat pet animal holding clean welcome sweet home board vector..

Вектор

Похожие изображения

Добавить в Лайкбокс

#28961343 - Dog and cat set Collection of vector pets icon silhouette

Вектор

Похожие изображения

Добавить в Лайкбокс

#45588938 - cat set

Вектор

Похожие изображения

Добавить в Лайкбокс

#33223647 - Fashion portrait of hipster cat in glasses in the form of stars..

Вектор

Похожие изображения

Добавить в Лайкбокс

#43647116 - Vector image of a big set of cat icometric icons

Вектор

Похожие изображения

Добавить в Лайкбокс

#30451601 - Close-up portrait of hairless Sphinx cat on black background..

Вектор

Похожие изображения

Добавить в Лайкбокс

#39352737 - Black Cat with Green Eyes Vector Illustration

Вектор

Похожие изображения

Добавить в Лайкбокс

#43008070 - Black cat in different poses. Vector cartoon set

Вектор

Похожие изображения

Добавить в Лайкбокс

ru.123rf.com

Бесплатный вектор на тему кошечек

Кто не любит кошечек? В Интернете эти животные вообще почитаются как священные коровы в Индии. Мы тоже считаем, что котами ни один дизайн-проект не испортишь! Поэтому сегодня мы собрали бесплатный вектор, посвященный нашим теплым, пушистым и своенравным братьям младшим.